字母异位词分组

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

示例 2:

输入: strs = [""]
输出: [[""]]

示例 3:

输入: strs = ["a"]
输出: [["a"]]

提示：

• 1 <= strs.length <= 104

• 0 <= strs[i].length <= 100

• strs[i] 仅包含小写字母

解题思路

排序哈希

核心思路：利用哈希表，将排序后的字符串作为键，原字符串作为值分组存储。

1. 排序法：对每个字符串排序后，异位词的排序结果相同，可以作为哈希表的键。

2. 哈希映射：遍历每个字符串，将其排序后的结果作为键，原字符串添加到对应的列表中。

3. 结果收集：将哈希表的所有值（即分组后的列表）汇总返回。

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        HashMap<String, List<String>> map = new HashMap();
        for (int i = 0; i < strs.length; i++) {
            char[] chars = strs[i].toCharArray();
            Arrays.sort(chars);
            String key = new String(chars);
            List<String> list = map.getOrDefault(key, new ArrayList());
            list.add(strs[i]);
            map.put(key, list);
        }

        List result = new ArrayList<List<String>>();

        Set<String> keys = map.keySet();
        for (String key : keys) {
            result.add(map.get(key));
        }
        return result;
    }
}

盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

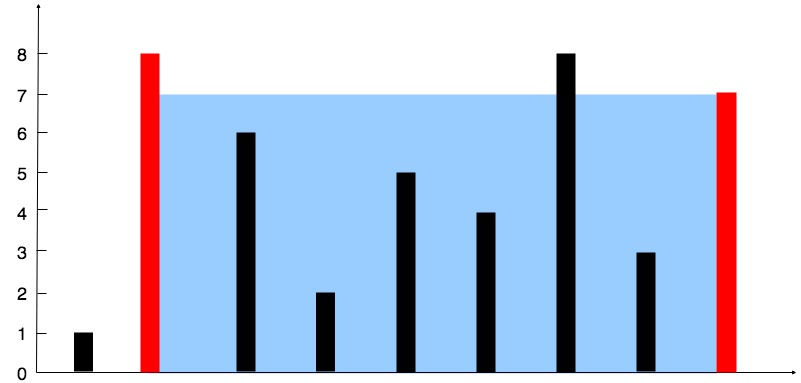
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

解题思路

双指针法/左右指针法

这个问题可以想象成用两条竖线围成一个水桶，水桶的容量由两条线中较矮的那条线的高度和它们之间的距离共同决定。我们需要找出能装最多水的两条线。

再偏题一句，能盛多少水由短板决定，而抛弃最黑暗的自己，才能有未来。

代码思路解析（双指针法/左右指针法）：

1. 初始化指针：
   用两个指针 left 和 right，分别指向数组的最左端和最右端。

   • left = 0（左边界）

   • right = height.length - 1（右边界）

2. 循环缩小范围：
   每次计算当前左右指针围成的“水桶”容量，然后移动较矮的那一侧的指针（因为移动较高的那一侧不可能让容量变大）。

3. 容量计算：
   容量 = 两条线的距离（right - left） × 两条线中较矮的高度（min(height[left], height[right])）。

4. 移动指针的逻辑：

   • 如果左边比右边矮（height[left] < height[right]）：
     此时左边的线限制了容量，即使右边的线再高也没用。于是将左指针右移，试图找到更高的左线。

   • 如果右边比左边矮（或相等）：
     同理，将右指针左移，试图找到更高的右线。

5. 更新最大容量：
   每次计算完当前容量后，与历史最大值比较，保留更大的值。

时间复杂度：O(n)，只需遍历一次数组。

class Solution {
    public int maxArea(int[] height) {
        int left = 0;
        int right = height.length-1;
        int max = 0;

        while(left < right){
            int temp = 0;
            if(height[left] > height[right]){
                temp = (right-left) * height[right];
                right--;
            }else{
                temp = (right-left) * height[left];
                left++;
            }
            if(max < temp) max = temp;
        }
        return max;       
    }
}